磁化强度-白红宇

磁化强度

阅读量：6510 次

发布时间：2019-06-24

本文共 3971 字，大约阅读时间需要 13 分钟。

在这篇文章内，与分别用与显示。例如，位置矢量通常用 $\mathbf{r}\,\!$ 表示；而其大小则用 $r\,\!$ 来表示。

磁化强度（英语：magnetization），又称磁化矢量，是衡量物体的的一个物理量，定义为单位体积的，如下方程：

${\mathbf {M))\ {\stackrel {def}{=))\ n{\mathbf {m))$ ；

其中， $\mathbf {M}$ 是磁化强度， $n$ 是密度， $\mathbf{m}$ 是每一个磁偶极子的磁偶极矩。

当施加外于物质时，物质的内部会被磁化，会出现很多微小的。磁化强度描述物质被磁化的程度。采用，磁化强度的单位是／米。

物质被磁化所产生的磁偶极矩有两种起源。

(1)

一种是由在内部的，由于外磁场的作用，其轨域运动产生的磁矩会做，从而产生的额外磁矩，累积凝聚而成。

(2)

另外一种是在外加后，物质内的粒子（原子核）发生“磁化”，趋于依照磁场方向排列。这些自旋构成的可视为一个个小，可以用表示，作为自旋相关磁性分析的描述。例如，用于现象中自旋动态的分析。

物质对于外磁场的响应，和物质本身任何已存在的磁偶极矩（例如，在物质内部的磁偶极矩），综合起来，就是净磁化强度。

在一个磁性物质的内部，磁化强度不一定是均匀的，磁化强度时常是的。

麦克斯韦方程组

描述 $\mathbf {B}$ 、 $\mathbf{H}$ 、 $\mathbf {E}$ 、 $\mathbf {D}$ 、 $\rho$ 和 $\mathbf {J}$ 的物理行为。这里会探索磁化强度 $\mathbf {M}$ 的角色和与这些物理量之间的关系。

磁感应强度、磁场强度和磁化强度之间的关系

主条目：

磁场强度 $\mathbf{H}$ 定义为

${\mathbf {H))\ {\stackrel {def}{=))\ {\frac {1}{\mu _{0))}{\mathbf {B))-{\mathbf {M))$ ；

其中， $\mu _{0}$ 是。

对于物质和物质， $\mathbf {M}$ 与 $\mathbf{H}$ 之间的关系通常是：

${\mathbf {M))=\chi _{m}{\mathbf {H))$ ；

其中， $\chi_m$ 是。

由于，物质的 $\mathbf {M}$ 与 $\mathbf{H}$ 之间并不存在关系。

磁化电流

在磁性物质内，“磁化电流”是总电流的一部分，又称为“束缚电流”，是由形成的。磁性物质内部的“束缚电流密度” ${\mathbf {J))_{b}$ 和“表面束缚电流密度” ${\mathbf {K))_{b}$ 分别为

${\mathbf {J))_{b}\ {\stackrel {def}{=))\ \nabla \times {\mathbf {M))$ 、

${\mathbf {K))_{b}\ {\stackrel {def}{=))\ {\mathbf {M))\times {\hat {n))$ ；

其中， ${\hat ((\mathbf {n))))$ 是垂直于磁性物质表面的单位矢量。

在麦克斯韦方程组内的总电流 $\mathbf {J}$ 为

${\mathbf {J))={\mathbf {J))_{f}+{\mathbf {J))_{b}+{\mathbf {J))_{P}$ ；

其中， $\mathbf{J}_f$ 是自由电流密度， ${\mathbf {J))_{P}$ 是电极化电流密度。

自由电流密度是由自由电荷形成的自由电流的密度。自由电荷不束缚于物质的原子的内部。

电极化电流是由含时 $\mathbf {P}$ 形成的：

${\mathbf {J))_{P}={\frac {\partial {\mathbf {P))}{\partial t))$ 。

静磁学

除去自由电流和各种含时效应，描述磁现象的麦克斯韦方程组约化为

${\mathbf {\nabla \cdot H))=-\nabla \cdot {\mathbf {M))$ 、

${\mathbf {\nabla \times H))=0$ 。

应用类比方法，与静电学问题类比：

${\mathbf {\nabla \cdot E))={\frac {\rho }{\epsilon _{0))}$ 、

${\mathbf {\nabla \times E))=0$ ，

静磁学的问题可以用静电学的方法来解析。在这里， $\nabla \cdot {\mathbf {M))$ 项目类比于 ${\frac {\rho }{\epsilon _{0))}$ 项目。

磁化动力学

主条目：磁化动力学

当思考尺寸和奈米时段的磁化作用时，含时磁化物理行为变得很重要。不单只是依著外磁场的排列，在物质内的单独的磁偶极矩会开始绕着外磁场，通过弛豫，缓慢地随着能量传输进入物质结构，达成与磁场线排列。

磁性物质

各种不同磁性的级列。

抗磁性

主条目：

抗磁性是物质抗拒外磁场的趋向，因此，会被磁场排斥。所有物质都具有抗磁性。可是，对于具有顺磁性的物质，顺磁性通常比较显著，遮掩了抗磁性。只有纯抗磁性物质才能明显地被观测到抗磁性。例如，元素和元素（、、等等）都具有显著的抗磁性。当外磁场存在时，抗磁性才会表现出来。假设外磁场被撤除，则抗磁性也会遁隐形迹。

在具有抗磁性的物质里，所有电子都已成对，内秉电子磁矩不能集成宏观效应。抗磁性的机制是电子轨域运动，用经典物理理论解释如下：

由于外磁场的作用，环绕着的电子，其轨域运动产生的磁矩会做，从而产生额外电流与伴随的额外磁矩。这额外磁矩与外磁场呈相反方向，抗拒外磁场的作用。由这机制所带来的与温度无关，以方程表达为

$\chi =-\ {\frac {\mu _{0}NZe^{2)){6m))\langle r^{2}\rangle$ ；

其中， $\mu _{0}$ 是， $Z$ 是原子数量密度， $Z$ 是， $m$ 是电子质量， $r$ 是轨道半径。 $\langle r^{2}\rangle$ 是 $r^{2}$ 的量子力学平均值。

特别注意，这解释只能用来思考。正确的解释需要依赖。

顺磁性

对于顺磁性物质、铁磁性物质、反铁磁性物质，磁化率与温度之间的理论关系。

主条目：

元素和除了、、以外的都具有顺磁性。在顺磁性物质内部，由于原子轨域或分子轨域只含有奇数个电子，会存在有很多未配对电子。遵守，任何配对电子的自旋，其磁矩的方向都必需彼此相反。未配对电子可以自由地将磁矩指向任意方向。当施加外磁场时，这些未配对电子的磁矩趋于与外磁场呈相同方向，从而使磁场更加强烈。假设外磁场被撤除，则顺磁性也会消失无踪。

一般而言，除了金属物质以外，顺磁性与温度相关。由于热骚动（thermal agitation）造成的碰撞会影响磁矩整齐排列，温度越高，顺磁性越微弱；温度越低，顺磁性越强烈。

在低磁场，足够高温的状况，根据居里定律（Curie's law）， $\chi$ 与绝对温度 $T$ 的关系式为

$\chi =C/T$ ；

其中， $C$ 是依不同物质而定的（Curie constant）。

铁磁性

主条目：

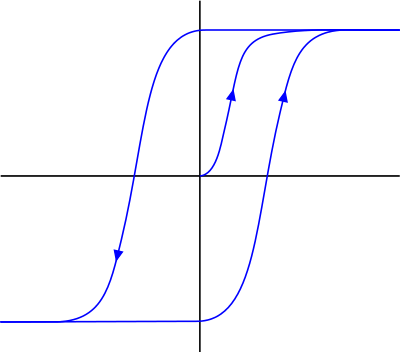
磁化强度（竖轴）与H场（横轴）之间的磁滞回路关系。

在铁磁性物质内部，如同顺磁性物质，有很多未配对电子。由于交换作用（exchange interaction），这些电子的自旋趋于与相邻未配对电子的自旋呈相同方向。由于铁磁性物质内部又分为很多，虽然磁畴内部所有电子的自旋会单向排列，造成“饱合磁矩”，与磁畴之间，磁矩的方向与大小都不相同。所以，未被磁化的铁磁性物质，其净磁矩与磁化矢量都等于零。

假设施加外磁场，这些磁畴的磁矩还趋于与外磁场呈相同方向，从而形成有可能相当强烈的磁化矢量与其感应磁场。随着外磁场的增高，磁化强度也会增高，直到“饱和点”，净磁矩等于饱合磁矩。这时，再增高外磁场也不会改变磁化强度。假设，现在减弱外磁场，磁化强度也会跟着减弱。但是不会与先前对于同一外磁场的磁化强度相同。磁化强度与外磁场的关系不是关系。磁化强度比外磁场的曲线形成了。

假设再到达饱和点后，撤除外磁场，则铁磁性物质仍能保存一些磁化的状态，净磁矩与磁化矢量不等于零。所以，经过磁化处理后的铁磁性物质具有“自发磁矩”。

每一种铁磁性物质都具有自己独特的。假若温度高过居里温度，则铁磁性物质会失去自发磁矩，从有序的“铁磁相”转变为无序的“顺磁相”。这是因为的无序趋向，大大地超过了铁磁性物质降低能量的有序趋向。根据居里-外斯定律（Curie-Weiss law），磁化率 $\chi$ 与绝对温度 $T$ 的关系式为

$\chi =C/(T-T_{c})$ ；

其中， $T_c$ 是（采用绝对温度单位）。

假设温度低于居里温度，则根据实验得到的经验公式，

$\Delta M(T)/M_{0}=\beta T^((3/2))$ ；

其中， $\Delta M(T)=M(T)-M_{0}$ 是磁化强度差， $M(T)$ 与 $M_{0}$ 是物质分别在绝对温度 $T$ 与 $0K$ 的磁化强度， $\beta$ 是依物质而定的比例常数。

这与布洛赫温度1.5次方定律（Bloch T3/2 law）的理论结果一致。

、、、与它们的、等等，这些常见的铁磁性物质很容易做实验显示出其铁磁性。

反铁磁性

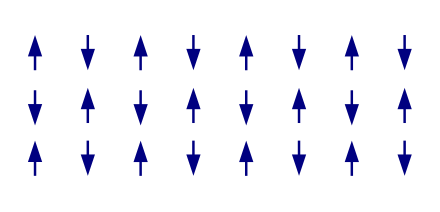
反铁磁性的有序排列

主条目：

在反铁磁性物质内部，相邻价电子的自旋趋于相反方向。这种物质的净磁矩为零，不会产生磁场。这种物质比较不常见，大多数反铁磁性物质只存在于低温状况。假设温度超过，则通常会变为具有顺磁性。例如，、、轻等等，都具有反铁磁性。

当温度高于 $T_{N}$ 时，磁化率 $\chi$ 与温度 $T$ 的理论关系式为

$\chi ={\frac {2C}{T+T_{N))}$ 。

做实验得到的经验关系式为

$\chi ={\frac {2C}{T+\theta ))$ ；

其中， $\theta$ 是依物质而定的常数，与 $T_{N}$ 差别很大。

理论而言，当温度低于 $T_{N}$ 时，可以分成两种状况：

假设外磁场垂直于自旋，则垂直磁化率近似为常数 $\chi _((\perp ))\approx C/T_{N}$ 。

假设外磁场平行于自旋，则在绝对温度0K时，平行磁化率为零；在从0K到奈尔温度 $T_{N}$ 之间，平行磁化率会从 $\chi _((\parallel ))(0)=0$ 平滑地单调递增至 $\chi _((\parallel ))(T_{N})=C/T_{N}$ 。

亚铁磁性

亚铁磁性的有序排列

主条目：

像铁磁性物质一样，当磁场不存在时，亚铁磁性物质仍旧会保持磁化不变；又像反铁磁性物质一样，相邻的电子自旋指向相反方向。这两种性质并不互相矛盾，在亚铁磁性物质内部，分别属于不同的不同原子，其磁矩的方向相反，数值大小不相等，所以，物质的净磁矩不等于０，磁化强度不等于零，具有较微弱的铁磁性。

由于亚铁磁性物质是。处于高时变磁场的亚铁磁性物质，由于感应出的很少，可以允许穿过，所以可以做为像隔离器（isolator）、循环器（circulator）、回旋器（gyrator）等等微波器件的材料。

由于组成亚铁磁性物质的成分必需分别具有至少两种不同的磁矩，只有化合物或合金才会表现出亚铁磁性。常见的亚铁磁性物质有（Fe3O4）、（ferrite）等等

超顺磁性

主条目：

当铁磁体或亚铁磁体的尺寸足够小的时候，由于热骚动影响，这些会随机地改变方向。假设没有外磁场，则通常它们不会表现出磁性。但是，假设施加外磁场，则它们会被磁化，就像顺磁性一样，而且磁化率超大于顺磁体的磁化率。

参阅

更确切地说，当 $\mu B/K_{B}T\gg 1$ 时，居里定律成立；其中， $\mu$ 是磁矩， $K_{B}$ 是。注释

参考文献

HP Meyers. Introductory solid state physics 2. CRC Press. 1997: 362; Figure 11.1. .

Catherine Westbrook, Carolyn Kaut, Carolyn Kaut-Roth. MRI (Magnetic Resonance Imaging) in practice 2. Wiley-Blackwell. 1998: 217. .

^ Chen, Chih-Wen, Magnetism and metallurgy of soft magnetic materials, Courier Dover Publications: pp. 1, 7–8, 12, 1977,

^ Kittel, Charles. Introduction to Solid State Physics 6th. John Wiley & Sons. 1986: pp. 299–302, 323–324, 330–335, 340–344, 351–352. .

Chikazumi, Sōshin; Chad Graham. Physics of ferromagnetism 2nd. Oxford University Press. 2009: 140–142. .

转载于:https://my.oschina.net/wangsifangyuan/blog/863544

你可能感兴趣的文章

麦克斯韦方程组

磁感应强度、磁场强度和磁化强度之间的关系

磁化电流

静磁学

磁化动力学

磁性物质

抗磁性

顺磁性

铁磁性

反铁磁性

亚铁磁性

超顺磁性

参阅

更确切地说，当 时，居里定律成立；其中， 是磁矩， 是。注释

参考文献

更确切地说，当 $\mu B/K_{B}T\gg 1$ 时，居里定律成立；其中， $\mu$ 是磁矩， $K_{B}$ 是。注释